1. [C++]백준 알고리즘 1260번: DFS와 BFS - 코딩도치

안녕하세요. 코딩도치 입니다~

 

오늘은 백준 알고리즘 1260번 DFS와 BFS 문제를 풀어보려고 합니다!

 

DFS, BFS는 코딩 테스트나 알고리즘 대회 같은 곳에 꼭 등장하는 단골손님입니다.

 

그러니까 꼼꼼히 공부하고 연습하는 것이 좋겠죠?

 

먼저 DFS, BFS가 무엇인지부터 살펴보겠습니다.

 

DFS(Depth-First Search) : 깊이 우선 탐색

BFS(Breadth-First Search) : 너비 우선 탐색

 

DFS, BFS 모두 그래프 탐색의 일종으로, 탐색하는 방식의 차이에 의해서 구분되는 것입니다.

 

아래 그래프를 예로 DFS와 BFS를 설명해 보겠습니다.(시작 정점 0)

 

 

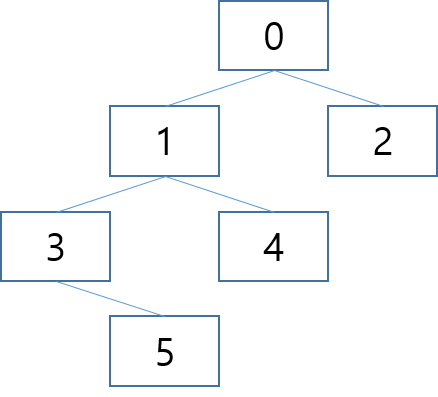
1. DFS(Depth-First Search) : 깊이 우선 탐색

 

결론적으로 말씀드리자면, DFS방식으로 위 그래프를 탐색했을 때 탐색 순서는 다음과 같습니다.

 

시작 정점 0 > 1 > 3 > 5 > 4 > 2

 

말 그대로 깊이를 우선적으로 탐색하는 방식입니다.

 

시작 정점에서 인접하는 정점들을 순회합니다.

 

0 인접 정점 : 1, 2

 

이때, 정점 1을 방문하였다면 정점 2를 방문하기 전에 먼저 정점 1에 인접한 정점들을 모두 방문하는 것입니다.

 

1 인접 정점 : 3, 4

 

그러면 정점 3을 방문하게 되고 또 정점 3의 인접 정점을 방문하게 되는 것입니다.

 

3 인접 정점 : 5

 

그렇게 모든 자식 정점들을 방문하였을 때 형제 정점을 방문하게 되는 것입니다.

 

3 형제 정점 : 4

1 형제 정점 : 2

 

위 그래프에서는 해당사항이 없지만, 형제 정점을 방문했을 때도 규칙은 변하지 않습니다.

 

만약 위 그래프에서 정점 4가 자식 정점을 가지고 있었다면,

 

4의 자식 정점을 모두 방문하고 1의 형제 정점인 2로 넘어가게 되는 것입니다.

 

이러한 DFS는 스택과 재귀 함수를 이용하여 구현할 수 있고, 모든 정점을 방문하고자 하는 경우에 주로 사용합니다.

 

2. BFS(Breadth-First Searcch) : 너비 우선 탐색

 

BFS방식으로 위 그래프를 탐색했을 때 탐색 순서는 다음과 같습니다.

 

시작 정점 0 > 1 > 2 > 3 > 4 > 5

 

너비를 우선적으로 탐색, 즉 시작 정점으로부터 가까운 정점들을 먼저 방문하는 방식입니다.

 

DFS와는 반대로 동일한 깊이에 있는 형제 정점들을 순차적으로 모두 방문하고 자식 정점으로 넘어가는 것입니다.

 

정점 1, 2 - 깊이 1

정점 3, 4 - 깊이 2

정점 5 - 깊이 3

 

이러한 BFS는 큐를 이용하여 구현할 수 있고, 최단 경로 혹은 임의의 경로를 찾고자 하는 경우 주로 사용합니다.

 

그럼 본격적으로 백준 알고리즘 1260번 문제를 풀어보도록 하겠습니다!

 

1260번 문제는 단순히 DFS, BFS를 구현해서 탐색 결과를 출력하는 문제입니다.

 

DFS와 BFS를 잘 이해하고 있다면 어려울 것이 없겠죠??

 

저는 DFS는 재귀 함수를, BFS는 큐를 이용하여 구현해 보았습니다.

 

#include <iostream>
#include <stack>
#include <queue>
#include <vector>
#include <algorithm>
 
using namespace std;
 
void dfs(int start, vector<int> graph[], bool check[]);
void bfs(int start, vector<int> graph[], bool check[]);
 
int main(){
    int N, M, V; // N: 정점의 개수,  M: 간선의 개수, V: 시작 정점 번호
    
    scanf("%d %d %d", &N, &M, &V);
    
    // 정점의 번호가 1부터 시작하기 때문에 N+1로 배열 할당
    vector<int> *graph = new vector<int>[N + 1]; // vector배열을 이용하여 그래프 구성
    bool *check = new bool[N + 1]; // 방문한 정점을 확인하기 위한 배열
    fill(check, check + N + 1, false); // check배열 초기화
    
    for (int i = 0; i < M; i++){
        int u, v; // u, v: 간선이 연결하는 두 정점의 번호
        scanf("%d %d", &u, &v);
        
        graph[u].push_back(v);
        graph[v].push_back(u);
    }
    
    for (int i = 1; i <= N; i++){
        /* 방문할 수 있는 정점이 여러 개인 경우에는 
        정점 번호가 작은 것을 먼저 방문해야 하기 때문에 sorting 필요*/
        sort(graph[i].begin(), graph[i].end());
    }
    
    dfs(V, graph, check);
    printf("\n");
    
    fill(check, check + N + 1, false);
    
    bfs(V, graph, check);
    printf("\n");
    
    return 0;
}
 
void dfs(int start, vector<int> graph[], bool check[]){
    // 재귀함수 이용
    if(!check[start]){
            check[start] = true;
            printf("%d ", start);
 
            for(int i=0; i<graph[start].size(); i++){
                //탐색 정점의 자식 정점 개수 만큼 반복
                dfs(graph[start][i], graph, check);
            }
    }
}
 
void bfs(int start, vector<int> graph[], bool check[]){
    //큐 이용 - 선입선출
    queue<int> q;
    q.push(start);
    check[start] = true;
    
    while (!q.empty()){
        int tmp = q.front();
        q.pop();
        printf("%d ", tmp);
        
        for (int i = 0; i<graph[tmp].size(); i++){
            //탐색 정점의 자식 정점을 큐에 순차적으로 쌓고, 방문 check
            if (check[graph[tmp][i]] == false){
                q.push(graph[tmp][i]);
                check[graph[tmp][i]] = true;
            }
        }
    }
}

 

감사합니다.